对于仿真分析来说，网格划分和细化是至关重要的一步，也是非常头疼的一步。网格质量的好坏直接影响到解算的精度和速度。

那么，什么样的网格是高质量的？如何才能划分和细化出高质量的网格？接下来，我们来聊一聊网格的划分和细化到底应该怎么做。

#1

越接近正多面体的网格，品质越好？

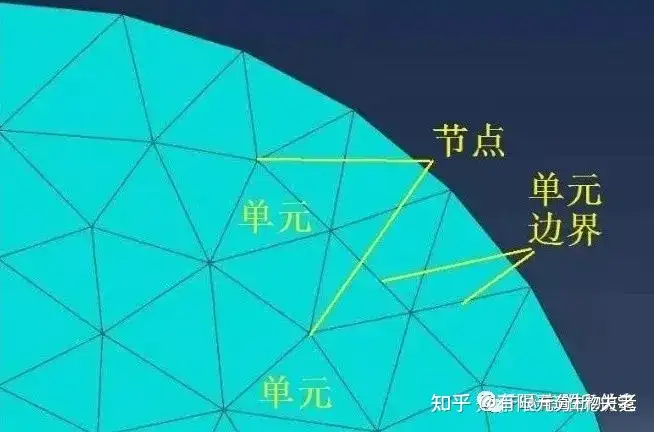
有限元分析划分网格的标准是单元属性（包括实常数）、几何模型的定义网格属性。定义网格的属性主要包括定义单元的形状、大小。

单元的形状对数值计算分析结果的精度有重要影响，而衡量单元形状的基本指标之一：长宽比（四边形单元的最长尺度与最短尺度之比），越趋近于1，计算结果会越精确；越偏离1，误差会越大。

也就是说越接近正多面体的网格品质越好。

举个例子，你选用了四边形形状的单元，那你得注意最好是正方形；如果选用的是三角形单元，那么最好是等边三角形。但即便长宽比无限趋近于1，结果的计算精度的误差也不容小觑。

那么，怎样才能得到更高精度的解呢？

答案是：细化网格。

#2

网格细化的“粗细”如何平衡？

按照常理，分析中使用的网格数量越多，计算精度也会相应提高，但很显然计算的时间也会越长。而实际工作后，你会发现企业一般会给你设置一个比较固定和紧凑的项目周期，如果你的分析计算时间过长，会严重拖延项目进度。

所以不管是数量少、品质差的网格，还是数量多、不经济的网格，都不是很可取。更恰当的方法是，我们在两者之间找一个平衡：用尽量少的网格得到最佳的目标值。

那么如何寻找一个平衡呢，我们可以从粗网格开始做起。也就是说：从大的网格单元开始做起。

一上来就使用细网格是很不科学的，因为你无法定性。那种花了大把时间画好细网格，最后却发现模型中的很多设置都错误了，这种感觉谁痛过谁知道。

而求解粗网格只需要较少的计算时间，虽然结果可能极其不准，但它可以作为一种粗略的验证手段，并能检查外加荷载和约束。从这个角度上说，粗网格算是节约了时间。

粗网格完成求解后，在进行下一步网格细化时，我们可以采用比较法来确定合适的网格数量。

当两个不同网格数量的计算结果差异不大时，意味着网格细化几乎可以被判定为合适了，模型已经收敛了。如果差异过大，那增加网格数量的工作还要继续，直至几个计算结果出现渐近。

#3

那么，网格细化有哪些常用技巧？

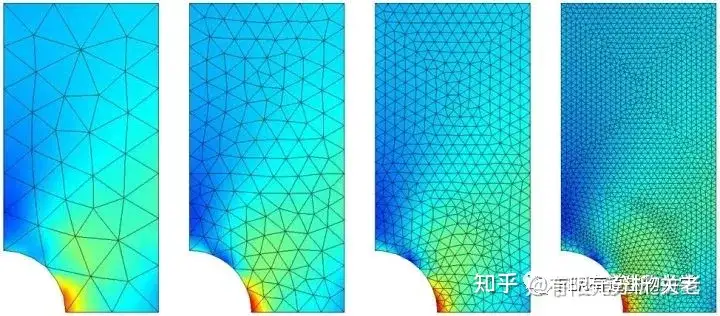
① 减小单元尺寸

减小单元尺寸是非常简单和直接的网格细化方法，它其实是对整体的网格划分尺寸进行设置，网格会不分区域进行整体细化。

▲图©COMSOL中国

在数据变化梯度较大的地方，比如应力集中点，这就会导致结果不太理想。反而只加密周围的区域，能够得到更加合理的结果。

▲图©COMSOL中国

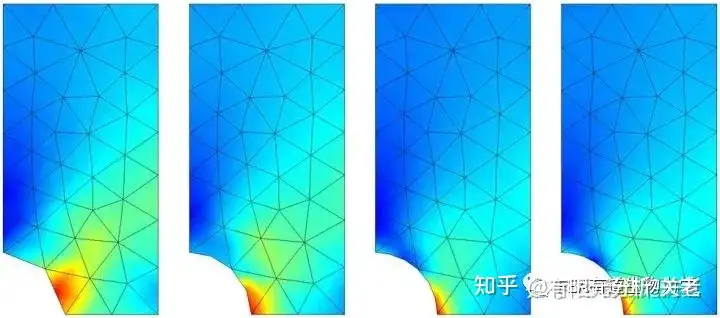
② 采用高阶单元

增加每个单元的节点数是实现“高阶单元”的方法，也是用ANSYS、ABAQUS等软件可以实现的方法。

通过提高节点数量从而提高插值形函数阶数，可以提高计算精度。这个方法非常适用于从外部获取了一个无法重新划分网格的有限元模型的情况。

它不仅帮我们省掉了重新划分网格的麻烦，还可以通过使用相同的有限元网格，只对单元阶数进行更改达到提高计算精度的目的。

▲图©COMSOL中国

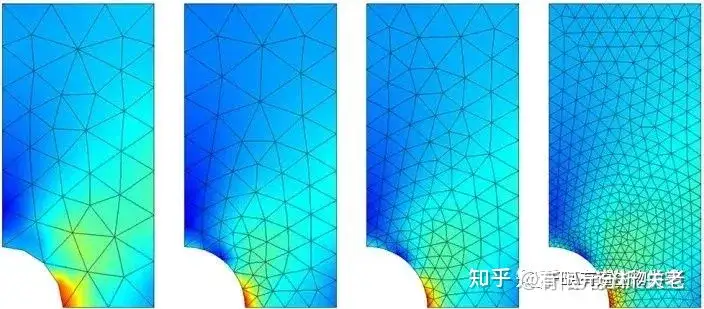
③ 自适应网格细化

自适应网格细化，是指通过事后误差估计，对计算结果误差较大的地方进行全局或局部网格优化。

好的有限元分析软件，都拥有自适应网格划分技术，能够自动分析计算曲率、找到沟槽、找到尖锐的夹角等，并能根据这些数据进行网格细化。

软件虽然替代人工完成了所有的网格细化工作，但也造成了显而易见的缺陷：用户失去了对网格的控制力。

▲图©COMSOL中国

④ 手动细化网格

这需要FEA人员有较强的分析能力，能够辨别哪些位置需要细化网格，哪些位置只需要粗略处理。

在热分析中，结构内部的温度梯度大时，要增加网格数量；静力分析中，计算变形所需的网格数量可以少一些；应力分析时，应力变化梯度比较大的地方，网格应该尽量的密。

手动细化网格对仿真分析的要求最高，但却是高效率的方式。

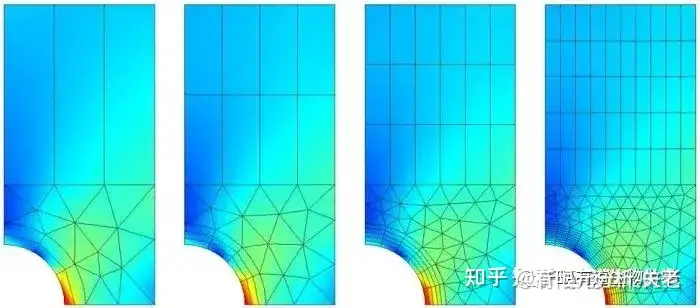
▲图©COMSOL中国

有限元网格的划分和细化，绝不止是不断细化网格这么简单。仿真分析人员应该综合考虑多方面的因素，才能做出经济又高质量的网格。