责任编辑:
长松落雪
时间:2023-03-12
来源:转载于:仿真学习与应用
责任编辑:
长松落雪
时间:2023-03-12
来源:转载于:仿真学习与应用
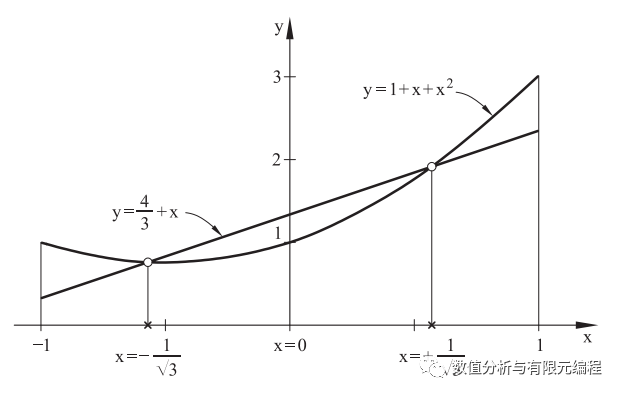
单元形函数的多项式阶数为p,则单元应变场(应力场)多项式的阶数为p-1阶或者p-2阶。要想得到精确的应力场表达式几乎是可能的,现在通过最小二乘估计来找一个最接近p阶多项式的p-1阶多项式。来看一个2阶多项式f(x)=1+x+x^2,设最接近此多项式的p-1阶多项式g(x)=a+bx。

两个函数的交点正好是我们所熟悉的高斯积分点,也就是说,在这些点附近,两个函数值最接近,在高斯积分点上,函数值是相等的。
再来看一个3阶多项式f(x)=1+x+x^2+x^3,设最接近此多项式的p-1阶多项式
g(x)=a+bx+bx^2。

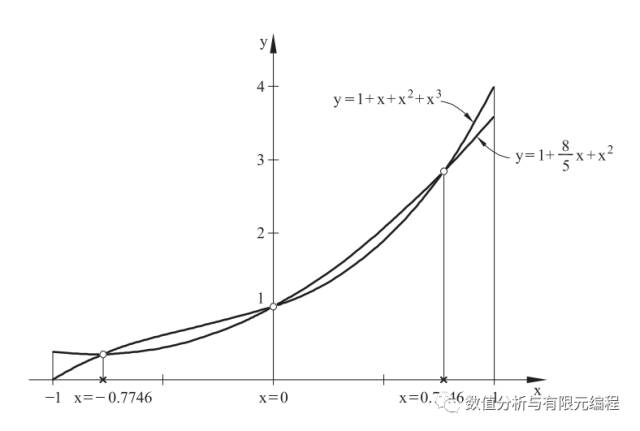
两个函数的交点还是我们所熟悉的高斯积分点!
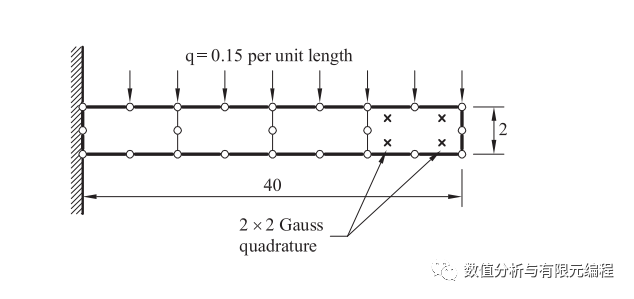
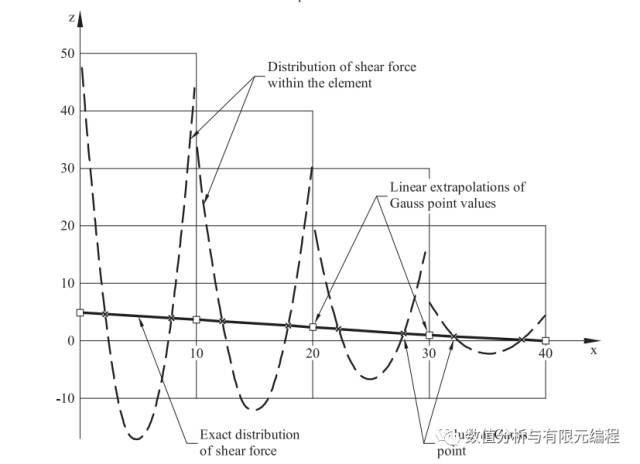
如图所示所示的悬臂梁,单元内的剪力与经典材料力学计算得到的剪力精确值的 交点正好位于每个单元的高斯积分点附近,也就是说,在高斯积分点计算单元应力,其误差最小!