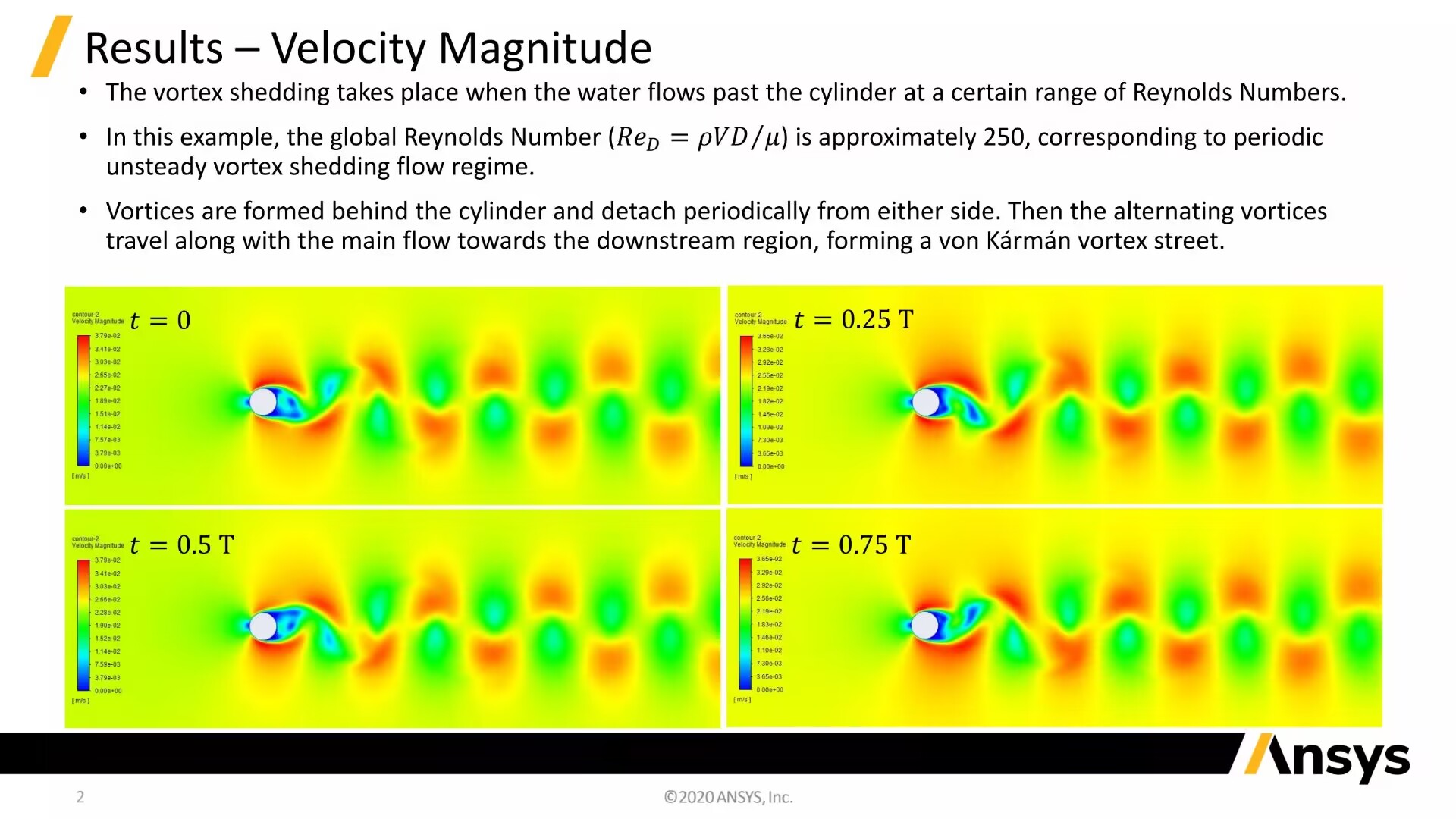
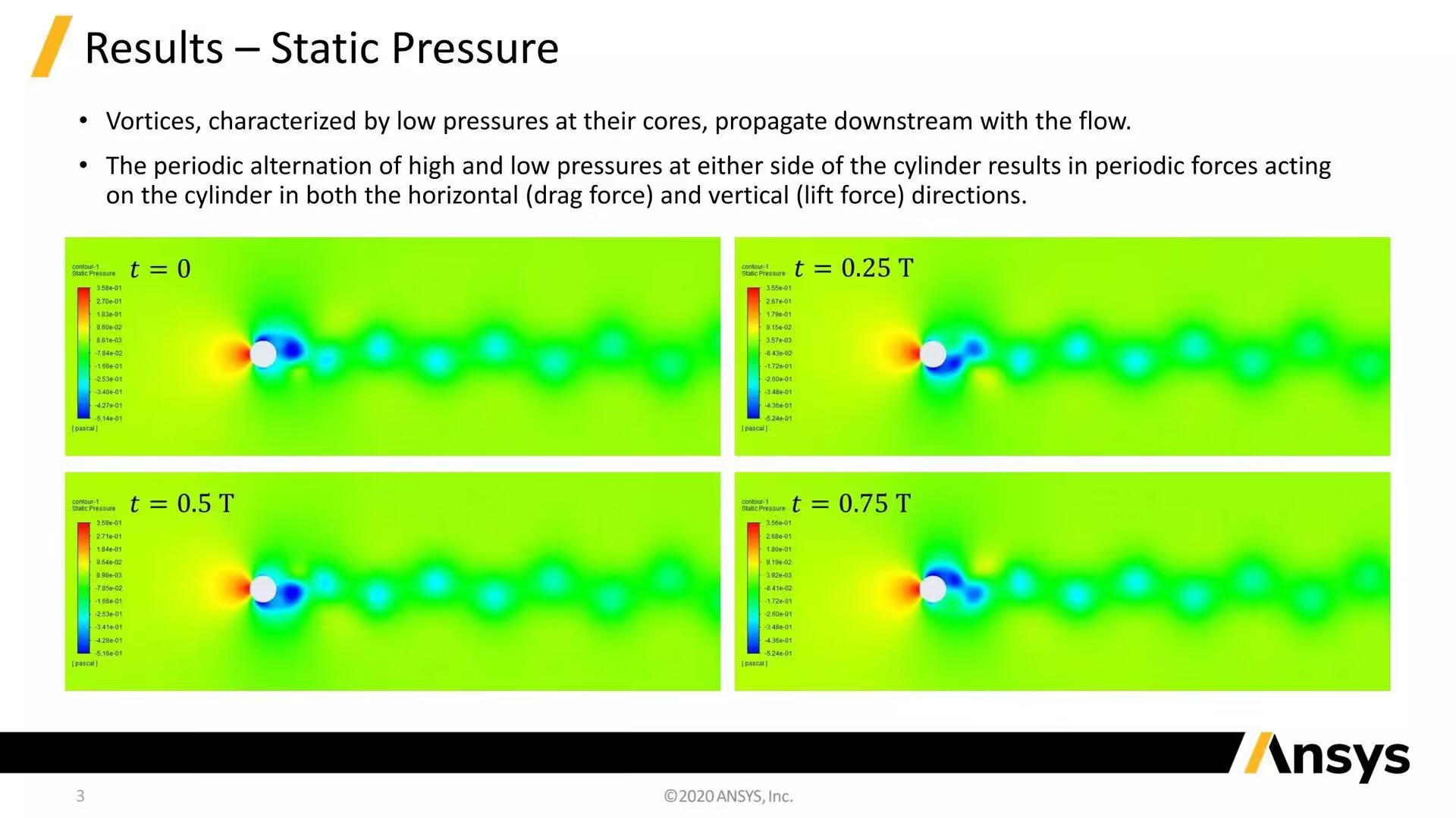
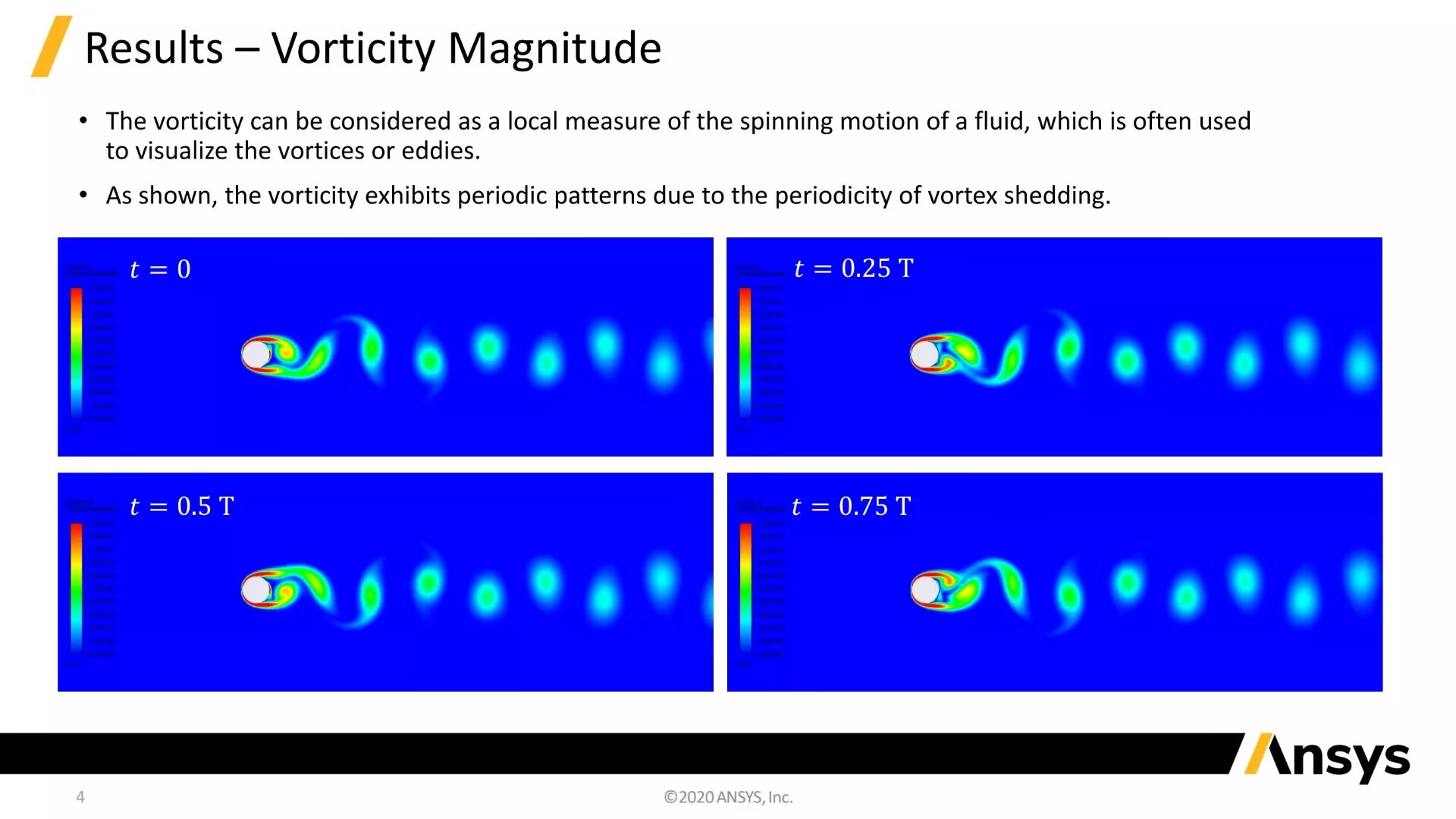
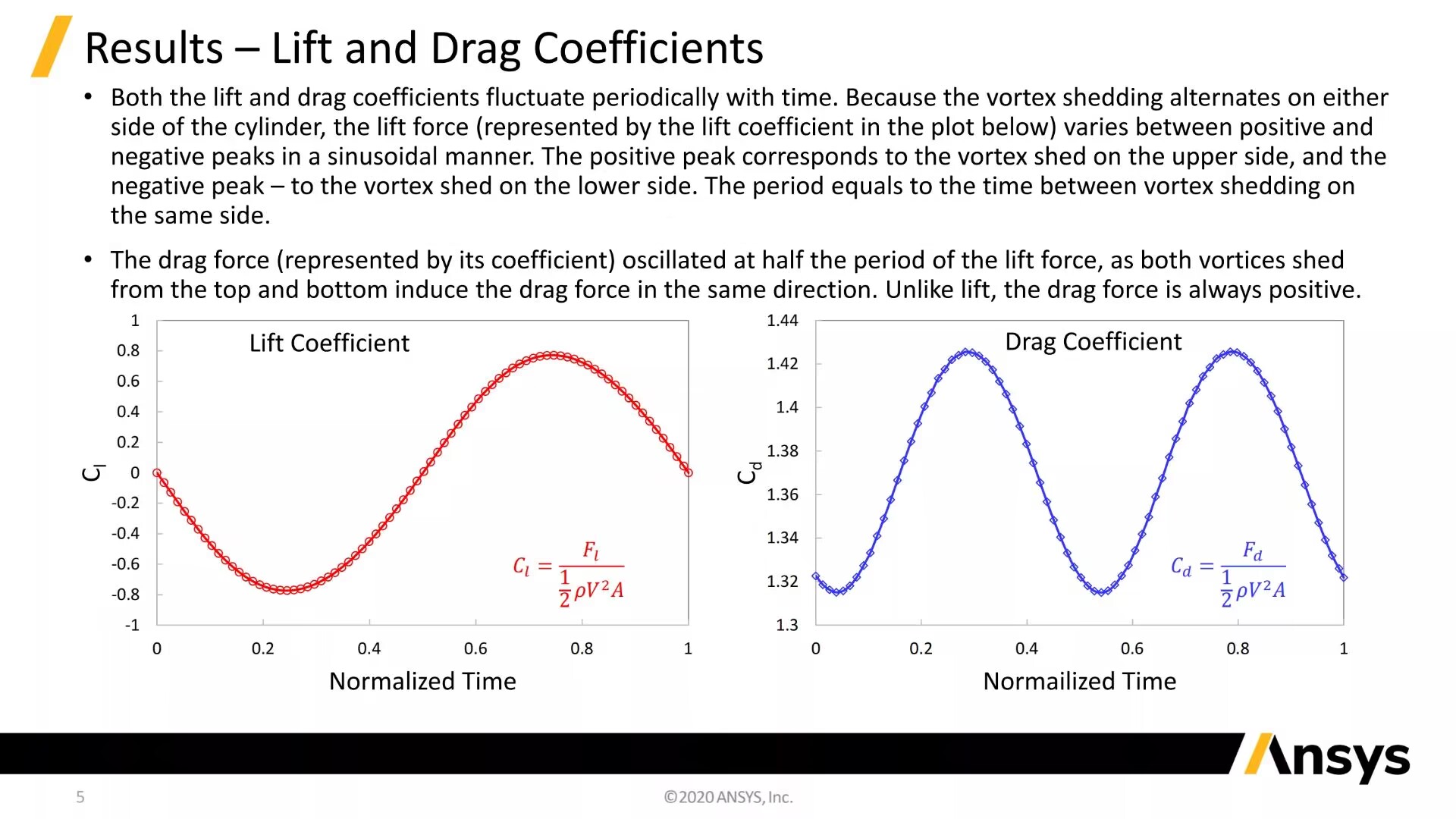
Fluent案例教程-圆柱绕流卡门涡街

物理上，所有的流体流动都是三维的，因此需要用三维模型来分析一般的流体，特别是那些涉及复杂几何形状的流体。然而，在某些情况下，可以作出适当的假设，将一个3d问题降低到2维(2 d)，以简化其分析或数值分析。一般来说，如果一个方向的流场梯度远小于另外两个方向的流场梯度，则可以用二维平面或轴对称假设来证明。例如，流过光滑球面的斯托克斯(或蠕变)流在周向上具有零梯度，因此对流动的轴对称假设是适当的。另一个经典的场景是两个平行平板之间的库埃特流，这可以近似一个二维平面模型。在这个例子中，一个非定常流动的二维数值模拟圆柱是完成的。采用二维平面假设是因为与其他两个方向相比，沿圆柱轴向的流动梯度可以忽略不计。通过将模型降低到二维，非定常周期性涡脱落过程可以以一种经济有效的方式进行模拟和分析，相比于一个完整的三维模型，这些结果可以用于生成一个冯卡门涡街的动画可视化形式。