湍流建模|02涡粘度模型-下
责任编辑：chjiegg
时间：2022-07-21
来源：转载于：技术邻——BB学长
责任编辑：chjiegg
时间：2022-07-21 来源：转载于：技术邻——BB学长
时间：2022-07-21 来源：转载于：技术邻——BB学长
分类：
技术分享
浏览量: 1028
导读：介绍涡粘模型-下。
k-w模型
通过输运方程求解湍流涡旋频率与k和
相关：
有两种方式可以推导得到方程：
与 方程一样，通过与k方程相似类比；
通过两者之间的关系，直接将k- 方程准确转换了k-
方程。
方程的形式为：
为湍流生成项；
,
-k-
方程与k-
方程推导其实是相同的，需要注意的是只针对特定实验数据校准模型，因此不能保证适用于所有的应用场合。
对于Vilcox形式的k-方程存在一个问题-方程求解的结果是基于剪切层外的值。
下图显示方程对混合层的预测：
速度U和无量纲化尺度 对
的取值具有强依赖性；
湍动能的变化非常剧烈。 当然这些是属于标准Wilcox模型的数学特征，这也是k-
模型相比于其的优势。
k-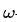
模型的优势在于：
与k- 模型相比，k-
模型在处理近壁面流动行为时，不会引入非线性项；
兼容层流湍流过渡建模，更适合分离流中的逆向压力梯度。不足在于：
（作为补充说明）
当湍流非常接近壁面时，湍流会被壁面削弱，在该区域 这个区域被称为粘性底层，近壁面的湍流模型需要有所调整。 在推导湍流模型时，没有考虑分子粘度，而是将其认为完全湍流，但是近壁面情况并非如此，因此需要进行修正。 这些修正被称为低雷诺数模型，但这里的雷诺数指的是湍流雷诺数 并非流动雷诺数。也称之为粘度子层模型
在k- 模型中增加衰减函数（称为低雷诺数项）；
相比之下，k- 模型处理方式更加简单，直接通过
的边界条件。
低雷诺数k-e模型
观察上述方程，均含有低雷诺数项，用于近壁湍流添加阻尼，这里有三种不同的模型：
问题在于这三种模型对平板流是有效的，但对于更复杂的流动，求解将变得不稳定，导致很难求解，对时间步长，网格质量要求极高。正因如此低雷诺数模型一般没有在工业流动仿真中使用。
k-e模型-双层模型
在商业软件中使用的替代方案就是双层模型，它针对的是低雷诺数模型求解困难的问题。双层模型的含义是：在非常接近壁面的地方，就是蓝色区域，根据代数项做了一个关于
的假设，代数项与距离壁面的距离y有关：
通过这种方式处理，就可以得到近壁方程：
表示混合函数，在近壁地方将它们加入边界层中间，远离壁面的地方，又去除这些项，常见形式如下：
对湍流粘度，，采用同样的方式处理：
这种方式在FLuent中就是增强壁面处理（Enhanced Wall Treatment，EWT）。
但是这种方式有些复杂，如果自由流中的k值过低，就有可能造成混淆，比如在贴近壁面的地方，距离壁面的距离很小，就有可能趋于0，模型最终就会切回近壁公式。
因此双层模型对于近壁处理是一个相当有问题的方案，其替代方案就是方程。
k-w方程的近壁处理
无需类似于 k- 无需双层模型。
对方程添加了交叉扩散项，就可以积分到壁面。
w方程的积分平台
鉴于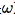
方程的两个优势：可靠的壁面处理和逆向梯度流中更优异的行为，可以围绕
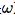方程组合湍流建模方案。
总结
Boussinesq假设是工业湍流建模的关键元素之一； 一旦知道两个独立的尺度，就可以计算湍流粘度，因此我们自然得到两个方程模型； 文章展示了如何从Navier-Stokes方程出发，先推导k方程，再推导出k- 模型和k-
模型，然后为每一项建模；
k- 模型可能会是未来最有前途的模型
来源：转载于：技术邻——BB学长
回复：