时间:2021-03-24 来源:正脉科工 CAE
连续系统是由弹性体元件组成的,以下我们讨论理想弹性体的振动。所谓理想弹性体是指满足以下三个条件的连续系统模型:
- 均匀分布
- 各向同性
- 服从虎克定律
弹性体具有分布的物理参数(质量、阻尼、刚度),弹性体的空间位置需用无数多个点的坐标来确定。也就是说,弹性体具有无限多个自由度。
通过对一些简单形状的弹性体的振动分析,将会看到:任何一个弹性体具有无限多个自然频率以及与之相应的主振型,这些主振型之间也存在着关于质量和刚度的正交性。弹性体的自由振动也可以表示为各主振动的线性叠加,对于弹性体的动响应分析主振型叠加法仍然是适用的。
弦的振动
波动方程
设理想柔软的细弦张紧于两个固定点之间,张力为T跨长为l,弦单位长度的质量为ρ,两支点连线方向取为x轴,与x轴垂直的方向取为y轴,如图1。
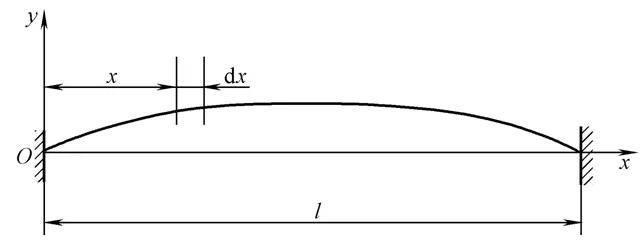
图1 弦振动示意图
设弦的振动发生在xoy平面内,弦的运动可表示为y= y(x,t) 。并假设弦的振动幅度是微小的,即y与∂y/∂x均为小量;在这些假设下,弦的张力T可近似地看作常量。再设重力与阻尼的影响均可略去不计。
在自由振动中,弦的微元dx的受力图,如图2,运动微分方程为
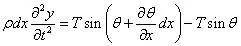
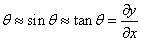
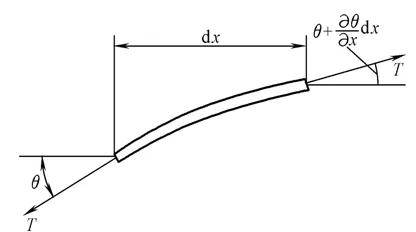
图2 弦振动示意图
故有
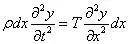
整理得
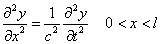
亦称为波动方程。其中c就是弹性波沿弦向的传播速度。
式中
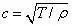
弦的运动还必须满足边界条件
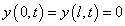
特征方程
描述弦振动的函数y(x,t) 可以分解为空间函数与时间函数的乘积,即
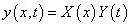
其中X(t)是振型函数,它表示整个弦的振动形态,而Y(t)表征点的振动规律。将上式代入
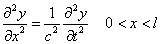
可得:
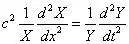
要使上式对任意的x与t都成立,必然是二者都等于同一个常数。设这一常数为α,得如下两个常微分方程
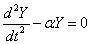

取α≡-ω²。于是,上述方程可改写为

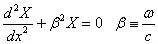
可解得
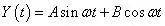
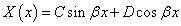
其中C 、D为积分常数,另外,由边界条件得
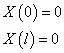
得

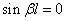
这就是弦振动的特征方程。由此可确定一系列特征值
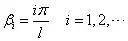
与此相应,可确定一系列特征函数,亦称振型函数。

与各个特征值相对应,可确定系统的各阶自然频率
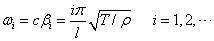
弦对应于各阶自然频率的主振动为

而弦的任意一个自由振动都可以表示为这些主振动的叠加,即有

其中各个Ai 与Bi 由运动的初始条件确定。
设在初始时刻t=0有
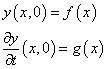
于是有
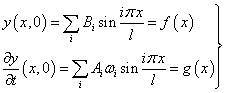
利用三角函数的正交性,可得
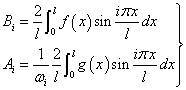
可见,张紧弦的自由振动,除了基频(最低频率)振动外,还包含频率为基频整数倍的振动。这种倍频振动亦称为谐波振动。
杆的纵向振动
设杆的横截面在振动时仍保持为平面并作整体运动。略去杆纵向伸缩而引起的横截面变形。
取杆的纵向作为x轴,各个截面的纵向位移表示为u(x,t),如图3。杆的微元dx在自由振动中的受力图也在图3中给出。
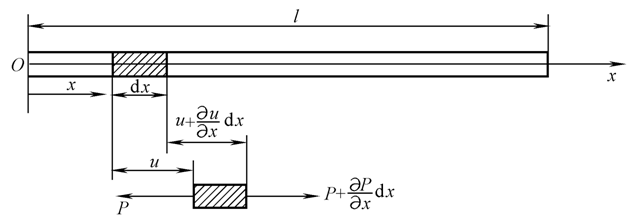
图3 等截面细直杆的纵向振动示意图
设杆单位体积的质量为ρ,杆长为l,截面积为A,材料的弹性模量为E。再设任一x截面处,纵向应变为ε(x),纵向张力表示为P(x) ;则由材料力学知
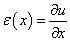
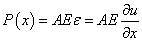
而在x=dx截面处的张力则为

列出杆微元dx的运动方程,得

整理得
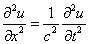
其中c²=E/ρ。
仍然采用分离变量法,将u= (x,t)表示为

得到类似于下式的常微分方程组

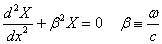
由此解得U(t) 与X(x) :

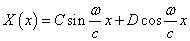
1. 两端固定的杆
这一情形与上节所述弦的振动相似。边界条件为
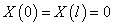
可得到
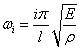
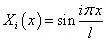
2. 两端自由的杆
这时,杆两端的应力必须为零,故边界条件为

由此得

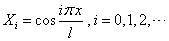
3. 一端固定一端自由的杆
这时,边界条件为

由此得
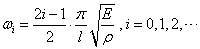

4. 一端固定一端弹性支承的杆

图4 一端固定一端弹性支承的杆示意图
设弹性支承刚度为k。这时,边界条件为
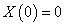
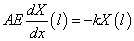
由此得

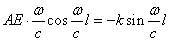
从后面一个方程可得

对应于给定的a值,不难找到各个固有频率ωi 的数字解。而与各个ωi 相应的振型函数为

轴的扭转振动
假设轴的横截面在扭转振动中仍保持为平面作整体转动。
取圆轴的轴心线作为x轴,图5轴任一x截面处的转角表示为θ(x,t)。设轴长为l,单位体积的质量为ρ,圆截面对其中心的极惯量矩为Ip,材料的剪切弹性模量为G。轴的扭转应变为∂θ/∂x,作用于微元dx 两截面上的扭矩分别为
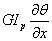
及
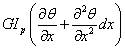
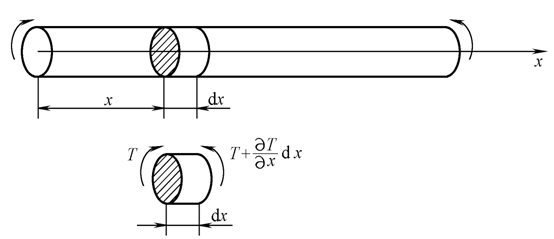
图5 轴扭转振动示意图
列出运动微分方程,可得

整理得
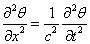
其中c²=G/ρ。这与前面得到的波动方程形式完全一样,故解的形式也一样。
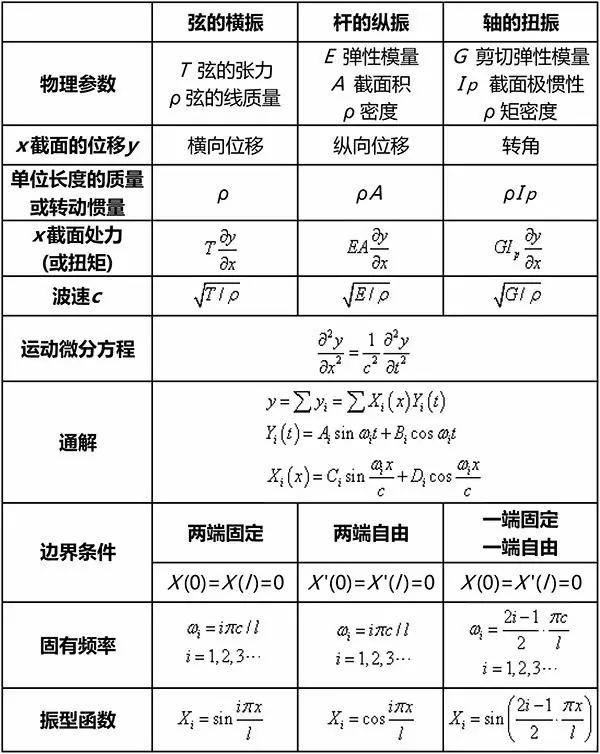
弦的横振、杆的纵振与轴的扭振都导致同一形式的波动方程。它们的运动具有共同的规律,如表1。
表1 弦的横振、杆的纵振与轴的扭振对比表
梁的弯曲振动
梁挠曲线的微分方程
假设梁具有对称平面,且在弯曲振动中梁的轴线(以下称为挠曲线)始终保持在这一对称平面内。取梁未变形时的轴线方向为x轴(向右为正),取对称面内与x轴垂直的方向为y轴(向上为正)。
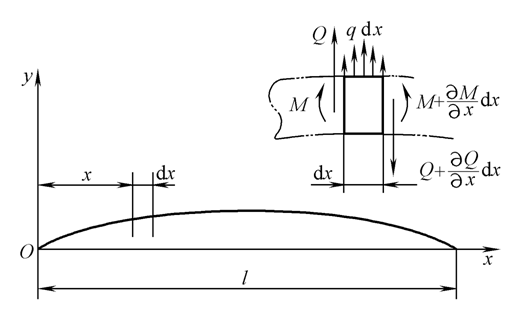
图6 梁弯曲振动示意图
梁在弯曲振动时,其挠曲线随时间而变化,可表示为
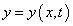
除了理想弹性体与微幅振动的假设外,还假设梁的长度与截面高度之比是相当大的。梁挠曲线的微分方程可表示为

即
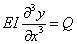
上式就是等截面梁在集度为q的分布力作用下的挠曲线微分方程。
弯曲振动的微分方程
应用达朗伯原理,在梁上加以分布的惯性力为

将上式代入方程
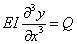
即得等截面梁自由弯曲振动的微分方程
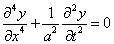
其中a²≡EI /ρ。上式是4阶偏微分方程,也需根据梁的支承情形附加适当的边界条件。所以,在数学上这类问题常称为偏微分方程的边值问题。
常见的边界条件
1. 固支端
该处挠度与转角都为零,即有
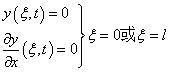
2. 铰支端
该处挠度与弯矩都为零,即有
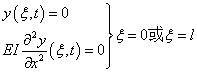
3. 自由端
该处弯矩与剪力都为零,即有

边界条件的分类:
- 几何边界条件:对挠度或转角的限制条件。
- 力边界条件:对弯矩与剪力的限制条件。
弯曲振动的微分方程的解
采用分离变量法。假设等截面梁自由弯曲振动的微分方程的解可表示为
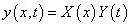
将式上代人等截面梁自由弯曲振动的微分方程,得
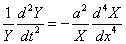
要使上式对于任何x与t值都能成立,必须使二者都等于同一个常数,和前面关于波动方程的讨论一样,只有当这一常数取负值时,才有对应于振动运动的解。故可以把这一常数记为-ω² 。
于是有

其通解为:Y(t)=Asinωt+Bcosωt

上式是一个4阶常系数线性常微分方程,它的特征方程为
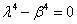
其特征值为
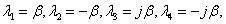
故方程

通解为

引用双曲函数,可将上述通解改写成

其中C1,C2,C3,C4为积分常数。
这时,边界条件相应地转化为
1. 固支端
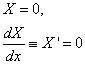
2. 铰支端

3. 自由端

在具体考察各种支承情形下梁弯曲振动固有频率与振型函数之前,先将边界条件中要用到的X(x)的各阶导数列出如下:

来源:正脉科工 CAE
点赞人: 王王木木
回复: